La estadística surge porque no se puede acceder a la totalidad de una población. Motivo por el cual se toma una muestra representativa de ésta para estudiarla y extrapolar los resultados al conjunto.
El Dr. Joaquín González Revaldería, Coordinador de Calidad del Hospital Universitario de Getafe, nos ponía como ejemplo la utilidad de un fármaco para disminuir la tensión arterial sistólica: dado que no podemos acceder a la totalidad de hipertensos a los que podría estar destinado dicho fármaco, realizaremos el estudio en una parte menor, pero representativa, de la población objetiva.
Como es evidente, siempre hay un cierto grado de incertidumbre al aplicar una generalidad a casos concreto que no se han particularizado. Sin embargo, si la pregunta de investigación es clara y concisa, la estadística puede otorgar resultados muy fiables y ajustados a la realidad de nuestro paciente. Cuanto más compleja sea la pregunta de investigación, más difícil será su tratamiento matemático y la interpretación de los resultados.
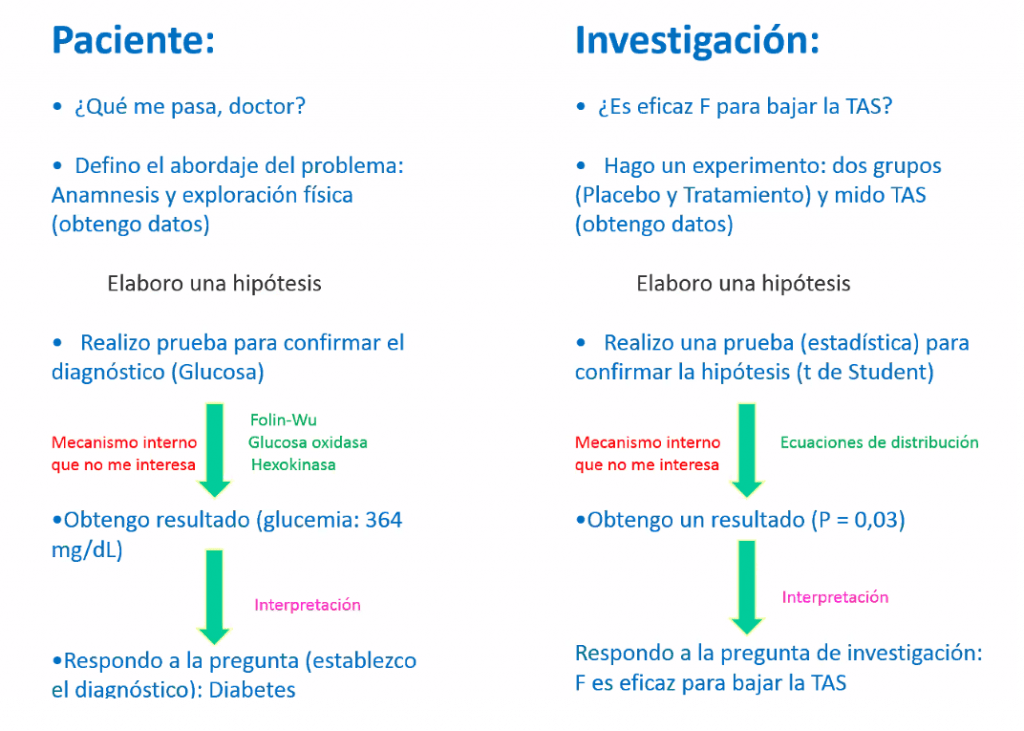
El médico realiza cálculos de este tipo, de forma involuntaria, continuamente. El paciente llega a la consulta con unos síntomas y quiere saber qué le pasa. El especialista realiza su exploración, empieza a trazar posibilidades, y a estudiar el comportamiento de las variables principales. A la vuelta de los resultados del laboratorio, el profesional tendrá ya unos valores exactos que le permitirán confirmar o refutar su hipótesis inicial.
Otra cuestión relevante en estadística es la forma de recoger los datos, que pueden ser de dos tipos: cualitativos y cuantitativos. Una variable cualitativa es aquella que describe las cualidades, circunstancias o características de un objeto o persona sin hacer uso de números ―fumador / no fumador―. Esta variable cualitativa puede ser también de tipo ordinal, no tiene números pero se establece una cierta gradación. El ejemplo más típico aquí sería la tira de orina, que puede ser cero, una cuz, dos cruces o tres cruces, y no quiere decir que entre cero y una cruz haya la misma proporción de leucocitos que entre una cruz y dos cruces. Es claro a partir de la tercera cruz, donde el valor posible de leucocitos es infinito en alternativas ―lo que sí sabemos es que a más cruces, más concentración de leucocitos en orina―.
A su vez, las escalas cuantitativas pueden ser de dos tipos: continuas, por ejemplo la concentración de X en un líquido biológico; o discretas, como el número de hijos. Es importante establecer bien la tipología de las variables a la hora de determinar cómo recoger y representar los datos, evitando representar variables cuantitativas como cualitativas. Por ejemplo, en un análisis de laboratorio, que nos permite conocer valores exactos, no debemos traducir esos valores a “Bajo” – “Medio” – “Alto” pues implicaría perder mucha información, y desajustar la exactitud que nos brinda la estadística.
La estadística descriptiva emplea valores de centralidad para contextualizar el resto de datos. A los parámetros que nos permitan saber si nuestros datos están muy agrupados o dispersos y, por tanto, si dicha centralidad es o no representativa en la muestra, es a lo que denominamos grado de dispersión. Las medidas de dispersión más utilizadas son: la varianza, la desviación típica y el coeficiente de variación.
Los valores que nos van a dar una idea de alrededor de en qué rangos se agrupan una serie de datos, son la media, la mediana y la moda. La media se define como la suma de todos los datos recopilados, partido del total de datos obtenidos. La mediana, es el valor que deja tantos resultados a su derecha como a su izquierda. La moda, que es el valor más frecuente en nuestra muestra, se utiliza muy poco en estadística porque tiene complejidad en su cálculo interpretativo.
Para saber cuál es la dispersión de los datos alrededor de la medida de centralización se emplea, o bien la desviación típica, o bien los cuartiles. En la mayoría de las distribuciones estos datos tienen una forma acampanada, simétrica, es a lo que denominamos campana de Gauss o distribución normal. Casi todas las distribuciones que nos encontraremos van a ser gaussianas, por lo que podremos emplear lo que se denomina estadística paramétrica. Una rama de la estadística inferencial que comprende los procedimientos estadísticos y de decisión que están basados en distribuciones conocidas. Este tipo de distribuciones normales se definen por la media de distribución, la centralización media, y la medida de dispersión o desviación típica.
Para las distribuciones no gaussianas tomamos la medida de centralización mediana y la media de dispersión intervalo intercuartílico. El rango intercuartílico es una medida de dispersión de un conjunto de datos que expresa la diferencia, la distancia entre el primer y el tercer cuartil. Utiliza la mediana como medida central y está considerado un estadístico robusto por su baja exposición a valores extremos.
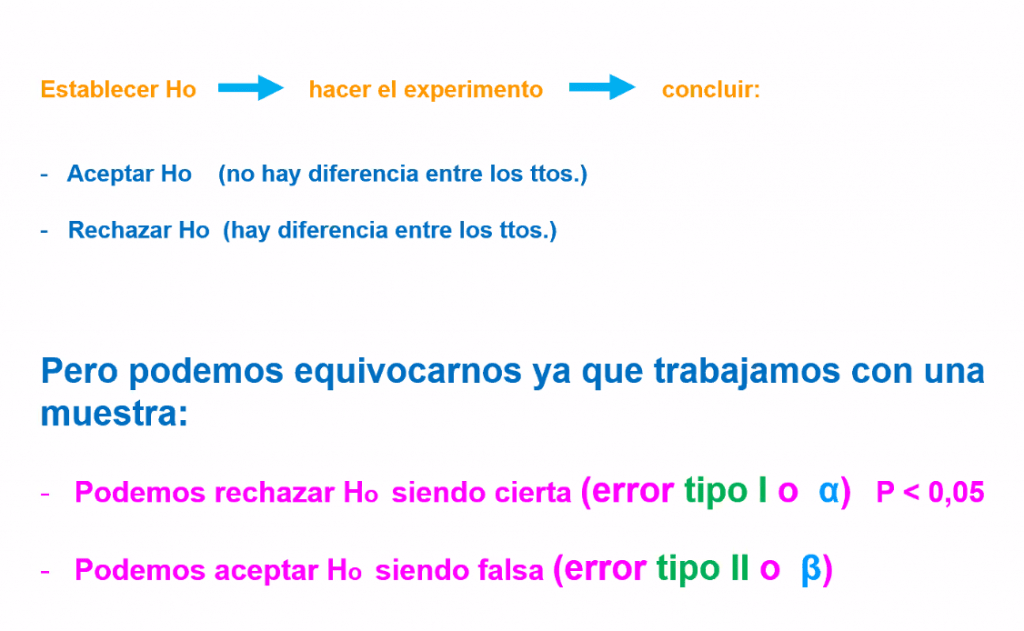
¿Qué debo tener en cuenta antes de realizar una prueba estadística? La formulación de la hipótesis. Clásicamente en medicina se establecen dos tipos de hipótesis: la hipótesis nula (H0) y la hipótesis alternativa. La hipótesis nula (H0) es la sentencia que el investigador pretender rechazar, o la que resulta de la afirmación contraria a la que ha llegado el investigador, en relación a algún o algunos parámetros de una población o muestra.
La probabilidad de equivocarnos en la afirmación o refutado de la hipótesis inicial es lo que conocemos como p, que por convención se establece que debe ser un valor inferior a 0,05 ―o lo que es lo mismo, el 5% de la muestra― para concebir el estudio como válido. Es decir, un valor de p < 0,05 es lo mismo que tener un Intervalo de Confianza igual o superior al 95%. Este valor p, o error tipo uno, determina la probabilidad de que un hallazgo de interés se haya alcanzado por casualidad. El error tipo 2 es aceptar la hipótesis siendo falsa: afirmar que un fármaco no tiene efecto cuando efectivamente lo tiene. Esto puede darse si la muestra es excesivamente pequeña, no representativa.
Para el tratamiento de las variables y la combinación cualitativa-cuantitativa en un mismo estudio, el Dr. Revaldería nos lo emplaza al próximo 31 de marzo para ver cómo operar, en la práctica, con el programa SPSS. Una plataforma software que ofrece análisis estadístico avanzado, una amplia biblioteca de algoritmos de machine learning, análisis de texto, extensibilidad de código abierto, integración con big data y un fácil despliegue en las aplicaciones.


